Coherent risk measure

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In the field of financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a risk measure ρ that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance.


Properties
Consider a random outcome X viewed as an element of a linear space of measurable functions, defined on an appropriate probability space. A functional → is said to be coherent risk measure for if it satisfies the following properties:^[1]

Monotonicity

That is, if portfolio Z₂ always has better values than portfolio Z₁ under all scenarios then the risk of Z₂ should be less than the risk of Z₁.^[2]

Sub-additivity

Indeed, the risk of two portfolios together cannot get any worse than adding the two risks separately: this is the diversification principle.

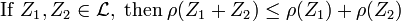
Positive homogeneity

Loosely speaking, if you double your portfolio then you double your risk.

Translation invariance

The value a is just adding cash to your portfolio Z, which acts like an insurance: the risk of Z + a is less than the risk of Z, and the difference is exactly the added cash a. In particular, if a = ρ(Z) then ρ(Z + ρ(Z)) = 0.