Hedge Fund Action Points to Further Pain for Yen ETF

November 26th 2013 at 2:30pm by Tom Lydon

Currency ETFs News:

• Gold’s Decline Good News for Aussie Bears
• Yen ETF Investors Say ‘Sayonara’ in Risk-On Environment
• WisdomTree: Interest Rate Differentials Imply the British Pound May Weaken

Japanese yen exchange traded fund traders could see more weakness ahead, with hedge funders betting on rising inflation in Japan and tapering in the U.S.
Futures traders pushed net shorts – bets that the yen will fall against the U.S. dollar – to the highest since July 2007, reports John Detrixhe for Bloomberg.
“Everybody likes dollar-yen higher,” Brad Bechtel, the managing director at Faros Trading LLC, said in the article. “And everyone has it on.”
George Soros reportedly made $1 billion between November 2012 to February 2013 on bets against the yen. Soros’ former chief strategist, Stan Druckenmiller, the founder of Duquesne Capital Management LLC, is “short some yen,” while being “long some Japanese” stocks.
The Bank of Japan has enacted an aggressive $70 billion monthly bond purchasing program since April to depreciate the strong yen currency, stimulate economic growth and reverse deflationary pressures. Consequently, the yen has declined 15% this year, the fastest drop since 1979.
The Bank of Japan has set an inflation target of 2% in two years. Governor Haruhiko Kuroda expects the target will be achieved sometime late in 2014 or early 2015. To put this in perspective, consumer prices have been declining 0.1% per year over the past 15 years. [Next Year Could be a 2013 Sequel for Japan ETFs]
Speculation that the Fed could taper its $85 billion a month bond purchasing program has also weighed on the yen against the U.S. dollar – tapering would reduce the supply of U.S. dollars in the economy and strengthen the U.S. dollar against foreign currencies. Fed minutes indicate they could reduce stimulus “in coming months” as the economy improves. [Yen ETF Investors Say ‘Sayonara’ in Risk-On Environment]
The yen traded as low as 101.92 per U.S. dollar Monday, the lowest since May. The Japanese currency sits around 101.32 per USD Tuesday.
The CurrencyShares Japanese Yen Trust (NYSEArca: FXY), which follows the price movement of the Japanese yen against the U.S. dollar, has declined 14.8% year-to-date.
As the yen continues to weaken and the Japanese economy expands, investors can take a look at yen currency-hedged Japan equity ETFs, like the WisdomTree Japan Hedged Equity Fund (NYSEArca: DXJ) and db X-trackers MSCI Japan Hedged Equity Fund (NYSEArca: DBJP), which have gained 35.6% year-to-date and 42.9% year-to-date, respectively. In comparison, the iShares MSCI Japan ETF (NYSEArca: EWJ), a non-currency hedged ETF, rose 24.3% year-to-date. [Good News for Japan ETFs: Goldman’s Still Bullish]
CurrencyShares Japanese Yen Trust

For more information on the yen currency, visit our Japanese yen category.
Max Chen contributed to this article. Tom Lydon’s clients own shares of DXJ.

The opinions and forecasts expressed herein are solely those of Tom Lydon, and may not actually come to pass. Mr. Lydon serves as an independent trustee of certain mutual funds and ETFs that are managed by Guggenheim Investments; however, any opinions or forecasts expressed herein are solely those of Mr. Lydon and not those of Guggenheim Funds, Guggenheim Investments, Guggenheim Specialized Products, LLC or any of their affiliates. Information on this site should not be used or construed as an offer to sell, a solicitation of an offer to buy, or a recommendation for any product.

Improving A Simple SPY Trading Model

Nov 26 2013, 09:34  |  about: SPY, includes: DIA, DOG, IWM, PSQ, QQQ, RWM, SH, SSO

BOOKMARK / READ LATER

Disclosure: I am short SPY. (More...)

In a recent article we explored some optimizations of a simple way to trade the S&P 500. In this article we'll take one additional step in developing a higher performance strategy to trade SPY that's still easy to implement.
We'll begin with an observation; this is not your father's or grandfather's market. We've gone from fractional values for shares to decimal and now we even have high frequency traders competing for fractions of fractions and a market that trades in microseconds. What's really been striking over the last 7-10 years in the markets is the explosive growth and proliferation of ETFs. Of particular interest are the original index centric ETFs that purport to accurately mimic the behavior of popular indexes like the S&P 500 (SPY) in 1993, the Dow Jones Industrial Average (DIA) in 1998, the NASDAQ 100 (QQQ) in 1999, and the Russell 2000 (IWM) in 2000 to name a few. What is even more interesting from a modeling and trading perspective was the introduction of inverse ETFs for each of these indexes that purport to accurately mimic shorting an index; these include (SH), (DOG), and (PSQ) in 2006, and (RWM) in 2007. For now we'll assume that, at least for short periods of time, these inverse ETFs do what they claim and reflect a true short position in their respective indexes to a reasonable degree of accuracy (they don't but the differences can be small for short time periods).
Let's start with a short review of the original strategy presented in a previous article, and the optimization proposed in the most recent article. The original strategy was a simple "skimming" algorithm; simply stated the strategy is you are long the S&P 500 when the price of the S&P 500 is above its 300-day Simple Moving Average [SMA], and you retreat to cash when the price is below the 300-day SMA. This is easily modeled using a spreadsheet and the results were a bit disappointing when viewed over the 20-year price history for the SPY ETF.
(click to enlarge)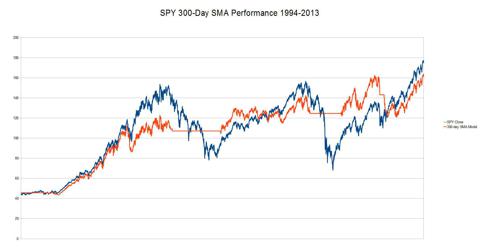
Performance Ratio = 0.91:1
The most recent article improved on this strategy by first optimizing the value of the SMA chosen to produce an optimal result for the 20-year period, and then by employing a leveraged ETF (SSO) to further increase overall gain. For this article we'll leave the leveraged ETFs out; my basic tenet is if you can get a model to work well with unleveraged ETFs then using leveraged ETFs will probably add both volatility and gain although you'll likely not see anywhere near the 2X gain they advertise. For this article all runs will be done close to close; i.e., the switch from long to cash or long to short will be done at the market close on the day the transition occurs.
(click to enlarge)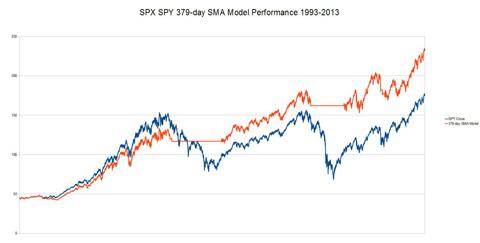
Performance Ratio = 1.35:1
So let's look a bit at algorithms, trading strategies and models. From our experience the basic idea is to look for an edge that persists over time and also works on multiple indexes and asset classes. Generally, the longer the time frame that's used in generating the model the better, but probably just as important is that the time frame chosen include at least 2 bull markets and 2 corrections to have some degree of confidence, going forward, that the model will continue to accurately follow the index and outperform whatever baseline you choose. Typically the baseline or benchmark is a simple buy and hold strategy in the underlying index.
A trading algorithm can take many forms and have a wide range of rules from simple to complex, but in the case of trying to beat an index the key metric is simply the performance ratio achieved. We define that as the total gain over a given time frame that the algorithm delivers divided by the total gain that a simple buy and hold strategy would deliver. The original and optimized algorithms in the earlier articles are what I call "skimming" algorithms, they're either 100% Long or 100% Cash, never Short. If you think about that you'll quickly realize the following:

1. When the algorithm is long the best you can do is simply track the underlying index. If the index goes up 1% you gain 1% and if the index goes down 1% you lose 1% (assuming there's negligible slippage in the ETF), but you cannot gain a performance advantage over the underlying index.
2. When the algorithm is in cash, this is the only opportunity in a skimming algorithm to gain a performance advantage over the index. If the index goes down 1% and the algorithm has you in cash, you effectively gain a 1% advantage over the index. Conversely, if the index goes up 1% and you're in cash you effectively lose 1% relative to the index.
3. Last, we'll introduce the ability, via inverse ETFs beginning in 2006/2007 to go short the index using a timing algorithm. In this case we're essentially "supercharging" a cash position; if the index goes down 1% and we're short presumably we'll gain 1% resulting in a 2% performance advantage. However, like all things in the market there's no free lunch. If the algorithm is wrong, and the index goes up 1% we'll lose 1% and effectively lose 2% relative to the index.

Basically, we need to be very careful in constructing an algorithm that can go short; get it right (and typically a 52-53% win rate is all that is required) and we can gain a nice advantage over a given buy and hold strategy or a long-cash strategy for an index, get it wrong and you'll have a model that loses money quickly.
To begin, we'll simply take our optimized 379-day SMA strategy and go short instead of cash when the price of the S&P 500 is below its 379-day SMA.
(click to enlarge)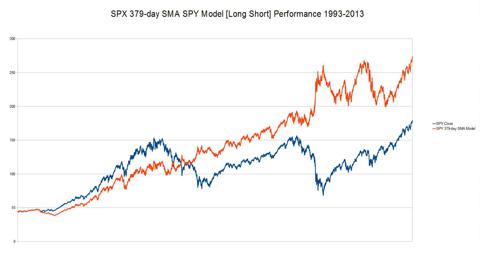
Performance Ratio = 1.53:1
We now have a somewhat higher performance ratio versus moving to cash, but what is also quickly apparent is that the algorithm produces a pretty volatile chart with a significant drawn down in the 2009-2011 region. So is there a way to improve on this, substantially reduce the volatility, and retain or improve performance?
Let's look at the 379-day SMA chart vs the S&P 500 and a couple of data points.
(click to enlarge)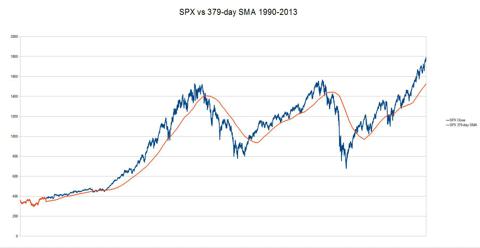
It's clear from a simple visual inspection that we have three peaks and two valley in the chart; what's also clear is that the 379-day SMA algorithm does a pretty decent job of getting into cash or short near a peak, but a pretty poor job of getting back to long near a bottom. Here's a couple of data points to illustrate:
2000 Peak 9/01/2000 1520.77
2000 379-SMA Crossover 10/10/2000 1387.02
Lag = 133.75 (8.8%)
2003 Valley 3/11/2003 800.73
2003 379-SMA Crossover 6/4/2003 986.24
Lag = 185.51 (23.2%)
2007 Peak 10/09/2007 1565.15
2008 379-SMA Crossover 1/4/2008 1411.63
Lag = 153.52 (9.8%)
2009 Valley 3/09/2009 676.53
2009 379-SMA Crossover 9/14/2009 1049.34
Lag = 372.81 (55.1%)
What we observe here is that while the lag from the peak to a crossing of the 379-day SMA from above is under 10%, the lag from a bottom to a crossing of the 379-day SMA from below is much larger. How do we fix this? One way is to look for a shorter duration SMA for the short side.
(click to enlarge)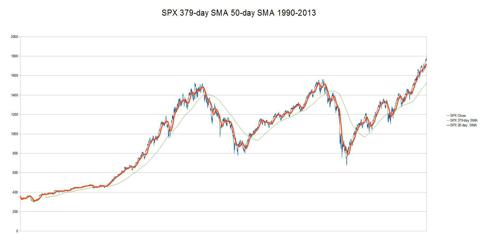
This chart shows both a 379-day SMA and a popular SMA for trading algorithms, the 50-day SMA.
So here's the algorithm we'll initially look at:
When the price of the S&P 500 (SPX) is above its 379-day SMA the algorithm is Long.
When the price of SPX is below its 379-day SMA then:

• if the price of the SPX is below its 50-day SMA then the algorithm is Short
• if the price of the SPX is above its 50-day SMA then the algorithm is Long

Let's see how that performs.
(click to enlarge)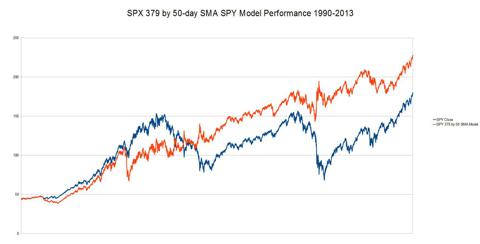
Performance Ratio = 1.26:1
So comparing this chart to the previous 379-day SMA Long Short Chart we've clearly reduced volatility but also sacrificed a lot of overall gain as we now have a lower Performance Ratio. So let's do some optimization on the short duration SMA (50-day) to see if we can find a set of better, optimal values. We'll write a little code and look at a range of both long duration and short duration SMAs in combination. We'll sweep from a long duration SMA of 375 to 425 and a short duration SMA from 50 to 100.
(click to enlarge)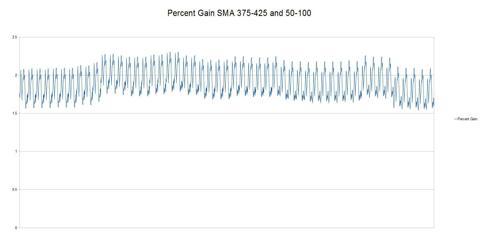
It turns out that there's two combinations that produce the same peak value:
Long Duration = 393 or 394 SMA
Short Duration = 77 SMA
What I believe is also important is that the Percent Gain chart is fairly consistent; there's a wide range of values that produce a decent gain (say > 200%) although the algorithm is sensitive to the low duration SMA. Next, let's look at the performance graph of 393 SMA by 77 SMA.
(click to enlarge)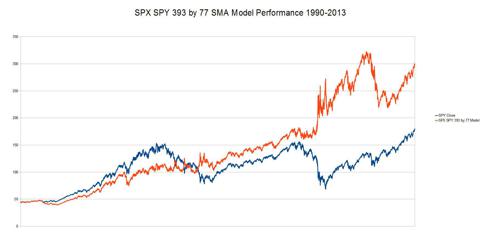
Performance Ratio = 1.66:1
So we now have more performance but at a cost of rather high volatility, especially in the 2011 region. There's one more "tweak" we can look at: instead of executing the transition when the price is below the long duration SMA (393) based on price moving up above a short duration SMA (77) let's look at using the slope (positive versus negative) of a short duration SMA to toggle the transition between short and long.
First, we'll need to sweep across SMA pairs using this new rule to find an optimal pair. For this study we'll sweep from a long duration SMA from 375 to 425 and a short duration SMA from 2 to 20.
(click to enlarge)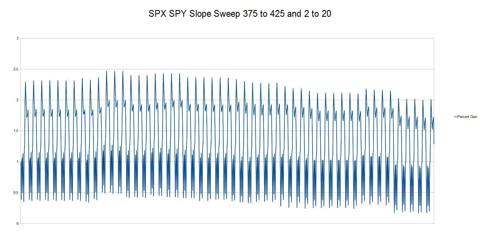
For this new algorithm, using the slope of a short duration SMA to transition from short back to long, the optimal values are 385 for the long duration SMA and 13 for the short duration SMA. The performance graph for this combination looks like this:
(click to enlarge)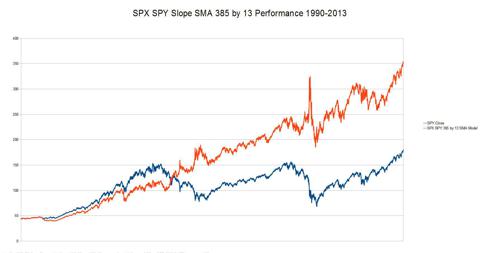
Performance Ratio 1.96:1
So now we've got a really nice performance ratio (nearly 2:1) with some volatility, especially in the 2008-9 downturn but overall a decent chart.
Last, I know I'll get questions about dividends. So here's a final chart of the SPX SPY 385 by 13 Slope SMA Model where the baseline is now the "Adjusted Closing Price" for SPY and we've accounted for the dividends when the model is Long.
(click to enlarge)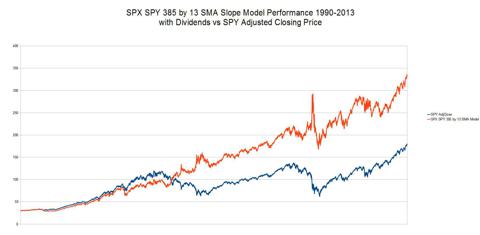
Performance Ratio 1.86:1

The ARIMAX model muddle

The ARIMAX model muddle

Published on 4 October 2010

There is often con­fu­sion about how to include covari­ates in ARIMA mod­els, and the pre­sen­ta­tion of the sub­ject in var­i­ous text­books and in R help files has not helped the con­fu­sion. So I thought I’d give my take on the issue. To keep it sim­ple, I will only describe non-​​seasonal ARIMA mod­els although the ideas are eas­ily extended to include sea­sonal terms. I will include only one covari­ate in the mod­els although it is easy to extend the results to mul­ti­ple covari­ates. And, to start with, I will  assume the data are sta­tion­ary, so we only con­sider ARMA models.
Let the time series be denoted by . First, we will define an ARMA model with no covariates:

   

where is a white noise process (i.e., zero mean and iid).

ARMAX mod­els

An ARMAX model sim­ply adds in the covari­ate on the right hand side:

   

where is a covari­ate at time and is its coef­fi­cient. While this looks straight-​​forward, one dis­ad­van­tage is that the covari­ate coef­fi­cient is hard to inter­pret. The value of is not the effect on when the is increased by one (as it is in regres­sion). The pres­ence of lagged val­ues of the response vari­able on the right hand side of the equa­tion mean that can only be inter­preted con­di­tional on the value of pre­vi­ous val­ues of the response vari­able, which is hardly intuitive.
If we write the model using back­shift oper­a­tors, the ARMAX model is given by

   

where and . Notice how the AR coef­fi­cients get mixed up with both the covari­ates and the error term.

Regres­sion with ARMA errors

For this rea­son, I pre­fer to use regres­sion mod­els with ARMA errors, defined as follows.

   

In this case, the regres­sion coef­fi­cient has its usual inter­pre­ta­tion. There is not much to choose between the mod­els in terms of fore­cast­ing abil­ity, but the addi­tional ease of inter­pre­ta­tion in the sec­ond one makes it attractive.
Using back­shift oper­a­tors, this model can be writ­ten as

   

Trans­fer func­tion models

Both of these mod­els can be con­sid­ered as spe­cial cases of trans­fer func­tion mod­els, pop­u­lar­ized by Box and Jenkins:

   

This allows for lagged effects of covari­ates (via the oper­a­tor) and for decay­ing effects of covari­ates (via the operator).
Some­times these are called “dynamic regres­sion mod­els”, although dif­fer­ent books use that term for dif­fer­ent models.
The method for select­ing the orders of a trans­fer func­tion model that is described in Box and Jenk­ins is cum­ber­some and dif­fi­cult, but con­tin­ues to be described in text­books. A much bet­ter pro­ce­dure is given in Pankratz (1991), and repeated in my 1998 fore­cast­ing text­book.

Non-​​stationary data

For ARIMA errors, we sim­ply replace with where denotes the dif­fer­enc­ing oper­a­tor. Notice that this is equiv­a­lent to dif­fer­enc­ing both and before fit­ting the model with ARMA errors. In fact, it is nec­es­sary to dif­fer­ence all vari­ables first as esti­ma­tion of a model with non-​​stationary errors is not con­sis­tent and can lead to “spu­ri­ous regression”.

R func­tions

The arima() func­tion in R (and Arima() and auto.arima() from the fore­cast pack­age) fits a regres­sion with ARIMA errors. Note that R reverses the signs of the mov­ing aver­age coef­fi­cients com­pared to the stan­dard para­me­ter­i­za­tion given above.
The arimax() func­tion from the TSA pack­age fits the trans­fer func­tion model (but not the ARIMAX model). This is a new pack­age and I have not yet used it, but it is nice to finally be able to fit trans­fer func­tion mod­els in R. Some­time I plan to write a func­tion to allow auto­mated order selec­tion for trans­fer func­tions as I have done with auto.arima() for regres­sion with ARMA errors (part of the fore­cast pack­age)

Understanding Tesla's Life Threatening Battery Decisions

Nov 22 2013, 00:52  | 99 comments  |  about: TSLA

BOOKMARK / READ LATER

Disclosure: I have no positions in any stocks mentioned, and no plans to initiate any positions within the next 72 hours. (More...)

In the last couple of months, electric cars from Tesla Motors (TSLA) have had three collision-related battery fires that were widely covered by the media. Last week, the NHTSA decided to conduct a formal investigation of these incidents. While Tesla's CEO Elon Musk immediately went on the offensive arguing that Tesla's BEVs have a lower fire risk than gasoline powered cars, the question an increasing number of investors are asking is "Why has Tesla had three battery fires in a fleet of 17,000 BEVs while Nissan hasn't had any fires in its fleet of over 90,000 BEVs?" The answer is simple. Tesla's battery decisions significantly increased battery risks for both the customer and the company.
My primary resource for the discussion in this article is a 2012 study published by the National Renewable Energy Laboratory titled "Vehicle Battery Safety Roadmap Guidance." Since the roadmap provides far more scientific detail than most investors need or want, I'll focus on the general themes that impact investment risk and leave the electrochemical and engineering minutiae for professionals.
The generic term "lithium-ion battery" includes at least a half-dozen varieties that range from relatively safe iron phosphate formulations to relatively unstable cobalt oxide formulations. I use the word relatively because no lithium-ion battery is 100% safe. All lithium-ion batteries will burn if the cell is punctured. In general, fires resulting from a punctured cell are the least violent. Lithium-ion batteries can also ignite spontaneously if debris left over from the manufacturing process pierces a 15- to 25-micron separator and creates an internal short circuit. In those cases, which are referred to as "field failure events," the internal short circuit ignites materials inside the cell and causes internal temperatures to spike to a few hundred degrees centigrade in seconds. At that point, the cell ruptures feeding additional oxygen to the fire. In rare unexplained cases, internal temperatures to spike to a couple thousand degrees centigrade in seconds, which suggests that thermite reactions might be taking place.
The failure mechanisms in lithium-ion batteries are not well understood because it's darned near impossible to extinguish a lithium-ion battery fire. In the event of a fire, the best first responders can do is try to cool the surrounding pack to keep the fire from spreading. What we do know is that punctured cells react less violently than cells that have a field-failure event and that field failure events are less violent than other failures that some experts attribute to thermite reactions.
Since the thermal energy released by a burning lithium-ion battery is up to three times greater than the electrical energy the battery could release in a normal discharge cycle, cell punctures and field failure events can be a very big deal as increased temperatures in one cell propagate to adjacent cells causing them to go into thermal runaway. The phenomenon is like lighting one side of a matchbook on fire. Once the first one goes, the others are sure to follow. One recent Tesla fire in Yucatan Mexico was captured in a YouTube video that shows how the process of lithium-ion battery fratricide unfolds in a large battery pack. The video begins with what appears to be a modest fire in a couple of punctured battery modules. As the temperature builds, other modules reach the thermal runaway point and explode. During the grand finale, several modules join the party and explode at the same time. If the incident didn't involve a $100,000 car and a real life accident, it would be a great special effect for Hollywood.
Tesla's first risky battery choice was picking cells with high energy density and a less desirable safety profile than the low energy density cells chosen by all of the other automakers.
Its second risky battery choice was ignoring the laws of large numbers.
Field-failure events are very rare and while I haven't been able to find detailed statistics for the 18650 cells Tesla buys from Panasonic, the NREL report noted:

"Field failures arising from manufacturing defects that cause internal short circuits have very low probabilities of occurrence (estimates for 18650-size cells that fail catastrophically are 1 in 10 million cells to 1 in 40 million cells). While this may be reassuring for manufacturers of portable electronics, EV and HEV battery packs may have thousands of cells and up to 1,000 times more stored energy, making even this small failure rate unacceptable."

The battery pack in a Tesla Model S uses about 7,000 high-energy 18650 cells that are more prone to field-failure events than safer lithium-ion chemistries. Since each cell in the battery pack represents an independent field failure risk, the risk of a catastrophic field failure event at the battery pack level is:

• One in 1,429 if you assume a 1 in 10 million risk at the cell level;
• One in 2,857 if you assume a 1 in 20 million risk at the cell level; and
• One in 5,714 if you assume a 1 in 40 million risk at the cell level.

Nissan, in contrast, uses 192 large format lithium-ion battery cells in the Leaf. That factor alone reduces its catastrophic battery pack failure risk by about 98%.
Some of the more troubling aspects of the NREL report included observations that:

"When discussing battery safety, it is important to understand that batteries contain both an oxidizer (cathode) and fuel (anode as well as electrolyte) in a sealed container. Combining fuel and oxidizer is rarely done due to the potential of explosion (other examples include high explosives and rocket propellant), which is why the state of charge (SOC) is a very important variable. Lower SOCs reduce the potential of the cathode oxidizing and the anode reducing. Under normal operation, the fuel and oxidizer convert the stored energy electrochemically (i.e., chemical to electrical energy conversion with minimal heat and negligible gas production). However, if electrode materials are allowed to react chemically in an electrochemical cell, the fuel and oxidizer convert the chemical energy directly into heat and gas. Once started, this chemical reaction will likely proceed to completion because of the intimate contact of fuel and oxidizer, becoming a thermal runaway. Once thermal runaway has begun, the ability to quench or stop it is nil."
"Although much study has gone into understanding and modeling the lifetime of cells with aging, little work has been done on the effects of aging on thermal stability and abuse tolerance."
"USABC goals, in line with the DOE research program for HEVs, are a calendar life of 15 years for HEVs and 10 years for EVs. A cycle lifetime of up to 1,000 cycles at 80% depth of discharge is also required. Little or no safety testing has been performed on cells approaching these lifetime limits. There are valid concerns about the stability of the active materials, separators, and possible reactions involving new degradation or contamination products."
"(H)igher energy cells have a stronger response to abuse events and usually have poorer safety performance."

Batteries in an electric car are maintained at a high state of charge to maximize driving range. Unfortunately, that practice also maximizes the potential for a field failure event. Since Tesla wanted its cars to have the longest possible driving range with the lowest possible battery weight, it chose a relatively unstable high-energy battery chemistry while its competitors who make electric cars with shorter ranges chose safer and more stable chemistries. Since Tesla wanted to keep its battery costs low and take advantage of a global capacity glut for 18650 cells, it decided to use 7,000 small format cells in its battery pack while more experienced automakers paid premium prices for large format automotive grade cells that reduce the impact of the law of large numbers.
All of Tesla's public talking points on the three fires focus on the collision-related nature of the battery pack failures. The statistics in the NREL report indicate that a catastrophic pack failure rate of 1 in 6,000 would be just about right if Tesla was using a safer low-energy chemistry like lithium iron phosphate.
If the NHTSA concludes that the fires were attributable to Tesla's risky choices of high energy density batteries in 7,000 cell packs instead of road debris, the impact on Tesla will be life threatening. The current market price of Tesla's common stock does not, in my opinion, reflect this real and substantial short-term survival risk.
Additional disclosure: I am a former director of Axion Power International and hold a substantial long position in its common stock. I currently serve as executive vice president of ePower Engine Systems, a privately held company that's developing an engine-dominant series hybrid drivetrain for heavy trucking.

Lien and Mean - How To Protect Your Property During a Construction Project

Lien and Mean - How To Protect Your Property During a Construction Project

January 26, 2005

Adam J. Basch

It should come as no surprise that if you hire a contractor to make improvements to your property, and you fail to pay him or her, the contractor has a right of action against you and may seek to place a lien upon your property. What is surprising, however, is that if this contractor fails to pay any of his or her subcontractors, one of them may be able to place a lien upon your property as well. In short, although you have paid your contractor all sums that are due, your property may still be at risk. The contractor’s failure becomes your liability.

As in most states, Massachusetts has a Mechanic’s Lien statute. This statute is codified in Massachusetts General Laws Chapter 254. In essence, the Mechanic’s Lien statute allows a contractor to place a lien upon property to secure his or her payment. This seems reasonable. What most people would view as unreasonable though, is to allow a subcontractor to place a lien upon your property, after you have paid the contractor in full. As with most areas of construction litigation, perils such as these can be avoided with a small amount of forethought and preventative action.

The statutory scheme for Mechanic’s Liens provides protective alternatives to avoid or dissolve any lien placed upon one’s property to those who are potentially subject to a Mechanic’s Lien. The first order of protection is to secure a no lien or blanket bond. Once filed, these bonds stand in the place of the real property. This means that liens of subcontractors attach to the bond as opposed to the real property. This remedy is codified in M.G.L. c.254, §12.

Another type of bond, codified in M.G.L. c.254, §14, is the target bond. This is used when the property is already the subject of a lien, and the property owner wishes to substitute a bond in place of the lien. This type of bond is most commonly used when a property owner wishes to refinance his or her property and is unable to do so because of a pre-existing lien. When a particular lien is “bonded off” by a target bond, the property owner must serve notice of the recording of the bond to the lien holder.

While the filing and posting of bonds can help alleviate some of the complications that arise from the filing of a lien, the best remedy for a property owner is to never have the lien arise in the first place. Rest assured that if the company issuing the bond eventually pays the subcontractor, it will seek reimbursement from you.

In Massachusetts it is illegal to require a contractor or subcontractor to execute a blanket lien waiver prior to performing his or her services. Although you cannot require a contractor or subcontractor to agree that they will not file a lien upon your property, you can require such a waiver at the time of payment. In most construction contracts, especially ones for new construction, payments are made to the general contractor at different intervals throughout the project. Prior to tendering any funds to the general contractor, the property owner should require that the general contractor, and all subcontractors who will perform services on the project, will agree execute a lien waiver. This protects you from essentially having to pay twice.

In order to ensure that all the applicable subcontractors have executed a lien waiver, you must first know what subcontractors are being retained. As such, all construction contracts should contain a provision that the general contractor will provide you with a list of the subcontractors that he or she plans to use on your job. Although this provides you with a limited degree of awareness, it is no substitute for first hand observation. In other words, visit the construction site often. Write down the names of any companies that appear on vehicles at the site, and do not be afraid to ask people who they are working for.

There is no such thing as being too proactive when it is your project. The old adage stands true here; an ounce of prevention is worth a pound of cure.

Adam J. Basch, Esquire, is an associate with Bacon & Wilson, P.C. He is a member of the Litigation Department with expertise in the areas of construction litigation, personal injury, general litigation and creditor representation. He can be reached at 413-781-0560 or abasch@bacon-wilson.com.
by: Adam J. Basch, Esq.

BusinessWest
January 2005